Chapter 19 Networks and ID

19.1 Overview and Learning Objectives

In this module, we will briefly discuss the concept of transmission networks and how that affects ID dynamics and control.

The learning objectives for this chapter are:

  • Know the how to define and measure transmission networks
  • Understand how different types of network structures affect ID transmission and control
  • Understand how transmission networks affect disease spread
  • Evaluate the impact of network structure on ID transmission

19.2 Introduction

ID spread along connections between infected and uninfected hosts. Those could be very close and defined connections, such as for sexually transmitted infections, or much less well-defined connections, such as a shared water or air source (e.g., cholera and influenza). If we want to account for these connections explicitly, we need to consider a conceptual framework that moves away from the compartmental approach. In the compartmental approach, all hosts with given characteristics (e.g., infected children) were lumped together, and no notion of connectivity was included. In contrast, a network perspective explicitly considers individuals and their connections.

19.3 Network Terminology

The basic building blocks of networks are entities and their connections. Those entities go by different, equivalent names, such as actor, node, vertex, site. Similarly, the connections have different, equivalent names, such as edge, link, bond, tie or connection. The different names stem from the fact that the network framework was developed independently in various scientific sub-fields.

Simple network diagram

19.4 Network Nodes

Usually, the nodes are individual hosts (e.g., humans). But that does not have to be the case. Nodes can also represent entities such as schools, cities, hospitals, etc. Simple networks only have one type of node, and more complicated networks can have different types of nodes. For instance, humans can be connected to specific places where they meet.

In their simplest form, nodes are only characterized by their connections, and they don’t have any other properties. In model simulations, it is possible to give nodes features such as age, gender, etc. and account for that when simulating ID spread.

19.5 Network Connections

What constitutes a connection in a network strongly depends on the question asked and the ID under consideration. Sexual networks connect people that have some form of sexual contact that was sufficient to transmit the disease in question. Similarly, social contact networks consider contacts between individuals in a social setting that allows for the transmission of an ID, e.g., close contact for transmission of a respiratory disease. Proximity networks can be built based on people frequenting the same locations. Connections can either be simple or have characteristics, which describe the relationship that exists between nodes. For instance, connections can have weights, with stronger connections between people that have closer or longer contacts. Connections can also have directions. For instance, if we wanted to model cholera transmission and had a network of villages, then a village upstream would have a connection pointing to villages downstream, but not the reverse. In other words, an ‘infected village’ upstream can infect a downstream village, but the opposite does not occur.

More complex network diagram showing different types of nodes and connections.

19.6 Network Characteristics

The initial study of a network often starts with the properties of the network itself, without considering any ID spread (yet). One of the most important characteristics of a network is the degree distribution of the nodes. This is simply a histogram of the number of connections that each node has. If connections have directions or there is more than one type of connection possible, then each one would have a histogram.

Another network characteristic is the ‘shortest path length,’ which measures the shortest distance of going from a particular node to some other node. Every node has a shortest path length to every other node (if 2 nodes are not connected because they belong to unconnected subparts of a network, the path length is considered infinite).

Many other network characteristics exist, the field of network analysis has proliferated in the last several years. If you want to learn more, (Newman 2013) is a useful resource. Many review articles on that topic also exist (Matt J. Keeling and Eames 2005).

It is important to understand that some characteristics are attached to individual nodes and some to the full network. For instance, every node has a number of degrees (connections), and the network has an overall degree distribution. Similarly, one can compute the mean shortest path length for each node and, if one takes another mean, a mean path length for the whole network.

19.7 Important types of networks

There are several types or classes of networks with specific characteristics that have been studied in great detail, either because they are analytically tractable or because of their real-world importance.

One of the best-studied networks is the random network. In this network, any 2 nodes have a fixed probability of being connected. For a network of N nodes and connection probability p, the average number of connections each node has (it’s degree) is (N-1)p. The degree distribution of the network is binomial, which for large networks becomes a normal distribution. That means most nodes have approximately the average number of connections. There are only a few nodes with substantially fewer or more connections.

Many real-world networks do not have the degree distribution found for random networks. It is often common that most nodes have very few connections, while a few nodes have many connections. This idea, for instance, underlies the superspreader concept. Such a distribution of connections can be well described by a scale-free network. In which case the degree distribution follows a power law, with most nodes having very few connections but a small number of nodes having very many connections.

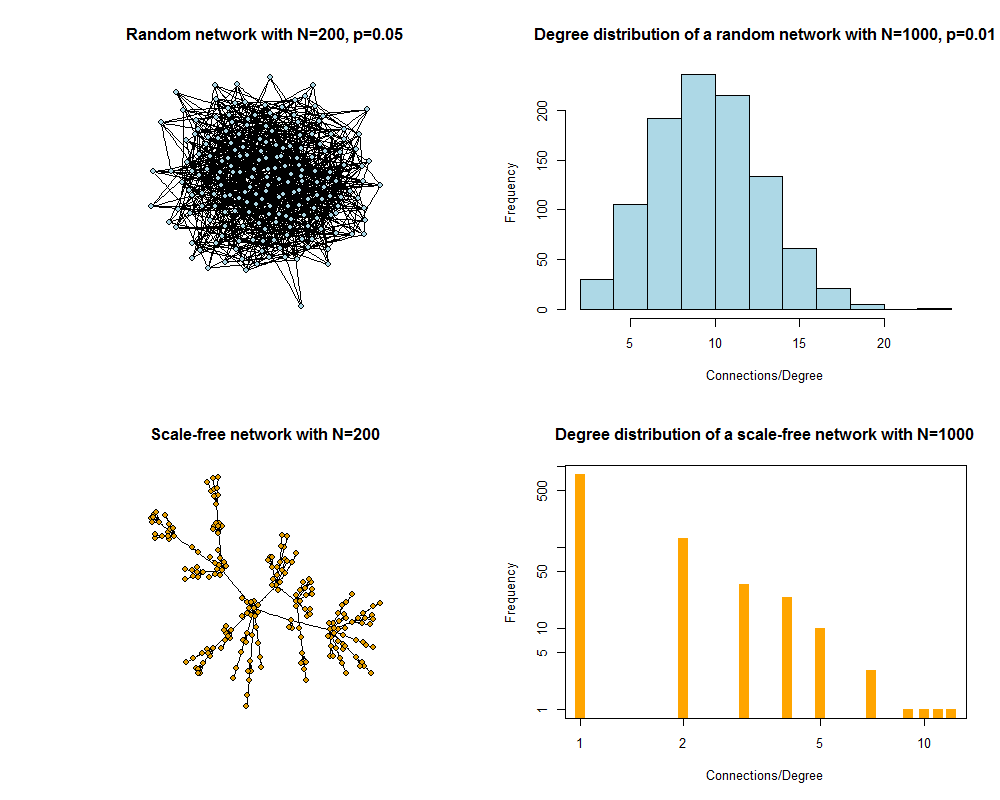
Random and scale-free networks and degree distribution.

FIGURE 19.1: Random and scale-free networks and degree distribution.

19.8 ID Transmission on Networks

The premise for ID transmission is that it can only occur along the connections of a network. As such, the structure of the network can strongly influence the dynamics of the ID. How exactly different characteristics of networks, such as the one discussed above and others, interact with the features of the ID to affect overall ID dynamics is an area that is currently heavily investigated. For some recent work on that, see (Bansal, Grenfell, and Meyers 2007).

19.9 Networks and ID Control

Knowing about the connection structure is necessary for ID control. Most obviously, if we are aware who the individuals are with many connections, we could target them preferentially and have a potentially larger impact compared to targeting random people. Other individuals that connect separate clusters of a network might also be prime targets. The challenge in real-world systems is to identify the individuals that should be targeted and being able to reach them, and in an outbreak situation, that would need to be done under time pressure. As such, while network theory has much to offer for control, it is still challenging to implement network-based intervention approaches in practice.

19.10 Modeling ID Transmission on Networks

Building and analyzing network models of ID transmission is generally more challenging than the compartmental modeling approach. For networks, we usually track individuals and as such the model becomes an agent-based model caring all the added complexity associated with agent-based modeling. It is also somewhat harder to analyze the results. Still, networks are a much closer approximation of real systems and have therefore seen increased use in the ID modeling community in recent years. With an increase in available data of the ‘network type’ (geocoded cellphone data) further increases in computational power and more sophisticated and efficient analysis approaches, it is quite likely that network-based methods will continue to grow in importance.

19.11 ID Transmission on Dynamic Networks

Most of the time, networks are considered static and do not change during the ID transmission process. However, this does not have to be the case and is often not realistic. The most detailed models allow for variations in the network through the making and breaking of connections and addition and loss (birth and death) of nodes. Implementing and analyzing models that have a dynamically changing network with the ID dynamics (and potential control measures) occurring ‘on top’ is technically challenging. Not too many of such models currently exist, but it is an area of active investigation by many, see (Bansal et al. 2010).

19.12 Summary and Cartoon

This module provides a brief discussion of transmission networks and how they impact dynamics and control of ID.

Computer viruses and human viruses are in many ways similar. [Source: xkcd.com](https://xkcd.com/350/).

FIGURE 19.2: Computer viruses and human viruses are in many ways similar. Source: xkcd.com.

19.13 Exercises

  • The online game VAX provides a nice interactive setting where you can explore vaccination on networks and how it can help reduce disease spread. Try to pass all levels.
  • Find a study that looked at the dynamics of an ID on a network. Summarize and discuss the study. Explain what findings in the study are due to the network approach. Discuss/speculate how results would be different if one were to ignore the network structure and instead used a compartmental model approach.
  • Read the article “Networks and epidemic models” by Keeling and Eames (Matt J. Keeling and Eames 2005). Find a recent paper that investigates a network for some ID and explain which data collection approach of the ones mentioned in section 3 (or a different one) was used. Also, discuss the structure of the network that was observed in relation to the ones described in section 5.

19.14 Further Resources

19.15 References