Model assessment using cross-validation
Overview
This unit discusses the idea of using existing data to assess how well a model might perform on external data.
Learning Objectives
- Understand the concept of cross-validation.
- Know that advantages and disadvantages of cross-validation.
Introduction
In the previous unit, we discussed the idea that using the data that was used to build and fit the model gives an overly optimistic view of model performance. Overfitting is a big risk and often leads to a model that does not perform well on new data.
Here, we’ll discuss a useful approach that can help minimize overfitting.
Honest performance evaluation
More data: The ultimate test is, of course, to check your model performance on newly collected data, or an existing, independently collected dataset. However, collecting or getting new data is not easy, and often you might not have a completely independent dataset that measures the same variables as the one you are trying to analyze/fit. Therefore, for the remainder of this discussion, we assume that getting more data is not an option. (Though if you have that option, certainly go for it!)
Reserving some data: If you have enough data, you can perform an evaluation of model performance that tries to imitate the idea of evaluating the model on newly collected data. What you do is that right at the start of your analysis, you set some of your data aside and do not look at it until the very end! A common fraction of data that is set aside is 20%-40%, but there is no clear rule. This data you set aside is called your test/validation data. You need to completely ignore that data and are not allowed to use it while doing any statistical model fitting. You then take the rest of your data, referred to as training data, and do all your model building and fitting and model choosing, etc.
At the end and only once at the very end do you run your model on the test data and compute the performance. The way you do this is to give your model the input variables (predictors) from the new data, ask the model to make predictions for the outcome, and use your metric/cost function to evaluate the performance of your model on that part of the data that your model has never seen before. This gives you an estimate of your model performance that is as honest as you can get without collecting new data. Be aware that even with this approach, you are likely still getting slightly better results than if you had evaluated your model on independently collected data (with somewhat different study design and data collection approaches). But in the absence of truly independent data, this is the best/most honest model performance evaluation you can do.
If you look at data analysis competitions such as Kaggle, this is how they operate. People need to submit their model predictions, and the model will be evaluated on a final dataset, only once, at the end of the competition. Whoever scores highest on that final dataset wins, no matter how well they did on the leaderboard.
While such a train/test split is an excellent thing to do, there are some constraints. First, you need to have enough data. If your dataset is small (<100-1000 observations, depending on the number of predictors and model complexity), then this approach will make you give away data that you need to build and fit your model reliably, and won’t provide robust insights. Second, you still need a way to decide which model to chose as your final model, and as mentioned above, using the one with the smallest cost function as evaluated on the data that was used to build the model is not good. An approach called cross-validation can help.
Cross-validation
Even with the train/test approach just described, you still need to figure out how to evaluate which model is best during the model building process. To that end, an approach called cross-validation has become very widely used and is currently - in my opinion - the best method to evaluate and choose your model.
Cross-validation (CV) is a reasonably straightforward approach. It mimics the train/test idea just described, but is now applied during the model fitting process. The idea is that you take the data you set aside for the model building process (i.e., your training data), and during the model building procedure, you repeatedly split your data into a portion to which you fit our model, and a portion which you use to evaluate model performance. You repeat this many times to get several samples and always use some portion of the data to fit the model, and the remaining part to evaluate it.
You might not be surprised to learn that this is another place where terminology is confusing and inconsistent. The words training data and test/validation data are used both for the initial split described above, and the split done in the CV procedure. One terminology is to call the splits done by CV the analysis and assessment portions of the data. This is shown nicely in this schematic. I will try to use that terminology, but I might not be consistent. And other materials you see/read certainly do not follow that terminology, as you will see already below.
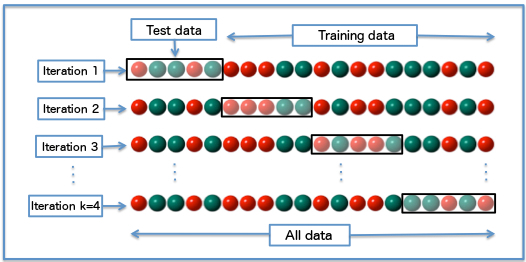
There are different ways to do the data splitting during cross-validation. A common setup is to randomly divide the data set into k blocks (called folds). You then use the data in all but one of the blocks to fit the model, then compute the cost function/performance metric (e.g., the RMSE) using the remaining block. You repeat that for all k blocks. The average value of the model performance over the k blocks is the target that you want to optimize. One usually chooses k = 5 or 10 blocks/folds, which has shown in simulation studies to give the best variance-bias trade-off. The figure shows an example of a 4-fold cross-validation for a categorical outcome (color of the balls). Note that this figure uses the train/test terminology for labeling the blocks, not the analysis/assessment terminology.
In addition to the standard way of splitting the data, there are different sampling variants. For instance, if you have longitudinal data, or otherwise data with structure, you might want to sample in a different way (e.g., sample the earlier times and predict later times). One variant of the cross-validation approach is the leave-one-out (LOO) cross-validation, which removes each data point one at a time as the test data and therefore performs the train/test part N times. You will also often see repeated cross-validation, which just adds another round of sampling on top to get better distributions (e.g., a 10-fold CV 10 times repeated gives 100 samples, which will be used to compute model performance).
Cross-validation works for most situations and is quite robust. It is also fairly easy to implement. Thus CV is a good default strategy. However, sometimes it is not possible or desirable to use CV. Occasionally, datasets are so small that you need all the data just to fit your model. Alternatively, your dataset might be large and/or your model complex, which might mean running a CV method takes too long. (Often, one can speed up things by down-sampling the data, using faster algorithms, or running code in parallel on a computer cluster.)
Cross-validation and model complexity
If you are mostly fitting GLM type models or other fairly simple models, you might wonder what I mean when I say during the model building/fitting process, since for a given simple model, there is just one set of model parameters that fits best, and that’s it. However, many more complex models have what is often referred to as tuning parameters. These are not part of the model structure (e.g., they are not the coefficients in front of your predictor variables), but they influence model performance. A great example are AI models, many of which easily have millions of parameters that need to be tuned to get good model performance. For those models, it is critical to evaluate model performance on data that is somewhat indepedent from the sample that is used to fit/tune/optimize the model.
To provide an analogy for a GLM, the number of variables you put in your model is somewhat similar. You learned that larger models fit better, so sticking more predictors into your model will give better performance (e.g., lower RMSE). However, this might lead to worse performance on independent data. You can then use something like CV to determine how many predictors might be best for your model.
Summary
Train/test data splitting and cross-validation are great approaches to more honestly assess the performance of a model. If your goal is to simply determine if there are patterns in the data you have, you might not need CV. But if you in any way have prediction as a goal, and want to understand if your model likely works in general - on data like yours, but not the one you used to fit the model - then you should use CV if you can.
Further Resources
Frank Harrell’s blog post discusses some of the potential caveats for using methods such as cross-validation.
Chapters 11 and 12 of the Tidy Modeling with R book provide additional discussion of the sampling/CV approaches. Another discussion of CV is chapter 30 of IDS.
Test yourself
What’s the name commonly given to the data you do your final model evaluation?One needs to use at least 10 folds/blocks in CV to get a reliable answer.
Using indepedently collected data to test model performance is better than using train/test or CV.
Practice
- Check publications in your area of interest, or look online on websites like Kaggle, to find an example of a data analysis that used the train/test and/or the CV approach. Read how the authors did things and what they found and report.